lunes, 2 de diciembre de 2013
Árbol AVL
Árbol AVL
El árbol AVL toma su nombre de las iniciales de los apellidos de sus inventores, Georgii Adelson-Velskii y Yevgeniy Landis. Lo dieron a conocer en la publicación de un artículo en 1962, «An algorithm for the organization of information» («Un algoritmo para la organización de la información»).
Los árboles AVL están siempre equilibrados de tal modo que para todos los nodos, la altura de la rama izquierda no difiere en más de una unidad de la altura de la rama derecha o viceversa. Gracias a esta forma de equilibrio (o balanceo), la complejidad de una búsqueda en uno de estos árboles se mantiene siempre en orden de complejidad O(log n). El factor de equilibrio puede ser almacenado directamente en cada nodo o ser computado a partir de las alturas de los subárboles.
Para conseguir esta propiedad de equilibrio, la inserción y el borrado de los nodos se ha de realizar de una forma especial. Si al realizar una operación de inserción o borrado se rompe la condición de equilibrio, hay que realizar una serie de rotaciones de los nodos.
Los árboles AVL más profundos son los árboles de Fibonacci.
Definición de la altura de un árbol
Sea  un árbol binario de búsqueda y sean
un árbol binario de búsqueda y sean  y
y 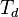 sus subárboles, su altura
sus subárboles, su altura  , es:
, es:
 un árbol binario de búsqueda y sean
un árbol binario de búsqueda y sean  y
y 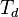 sus subárboles, su altura
sus subárboles, su altura  , es:
, es: si el árbol
si el árbol  contiene solo la raíz
contiene solo la raíz si contiene más nodos
si contiene más nodos
Las operaciones básicas de un árbol AVL implican generalmente el realizar los mismos algoritmos que serían realizados en un árbol binario de búsqueda desequilibrado, pero precedido o seguido por una o más de las llamadas "rotaciones AVL".
- Rotación simple a la derecha
De un árbol de raíz (r) y de hijos izquierdo (i) y derecho (d), lo que haremos será formar un nuevo árbol cuya raíz sea la raíz del hijo izquierdo, como hijo izquierdo colocamos el hijo izquierdo de i (nuestro i’) y como hijo derecho construimos un nuevo árbol que tendrá como raíz, la raíz del árbol (r), el hijo derecho de i (d’) será el hijo izquierdo y el hijo derecho será el hijo derecho del árbol (d).
- Rotación a la izquierda
De un árbol de raíz (r) y de hijos izquierdo (i) y derecho (d), consiste en formar un nuevo árbol cuya raíz sea la raíz del hijo derecho, como hijo derecho colocamos el hijo derecho de d (nuestro d’) y como hijo izquierdo construimos un nuevo árbol que tendrá como raíz la raíz del árbol (r), el hijo izquierdo de d será el hijo derecho (i’) y el hijo izquierdo será el hijo izquierdo del árbol (i).
Precondición : Tiene que tener hijo derecho no vacío.
- Rotación doble a la derecha
La Rotación doble a la Derecha son dos rotaciones simples, primero rotación simple izquierda y luego rotación simple derecha.
- Rotación doble a la izquierda
La Rotación doble a la Izquierda son dos rotaciones simples, primero rotación simple derecha y luego rotación simple izquierda.
Inserción
La inserción en un árbol de AVL puede ser realizada insertando el valor dado en el árbol como si fuera un árbol de búsqueda binario desequilibrado y después retrocediendo hacia la raíz, rotando sobre cualquier nodo que pueda haberse desequilibrado durante la inserción.
Proceso de inserción:
- 1.buscar hasta encontrar la posición de inserción o modificación (proceso idéntico a inserción en árbol binario de búsqueda)
- 2.insertar el nuevo nodo con factor de equilibrio “equilibrado”
- 3.desandar el camino de búsqueda, verificando el equilibrio de los nodos, y re-equilibrando si es necesario
Árbol binario de búsqueda auto-balanceable
Árbol binario de búsqueda auto-balanceable
En ciencias de la computación, un árbol binario de búsqueda auto-balanceable o equilibrado es un árbol binario de búsqueda que intenta mantener su altura, o el número de niveles de nodos bajo la raíz, tan pequeños como sea posible en todo momento, automáticamente. Esto es importante, ya que muchas operaciones en un árbol de búsqueda binaria tardan un tiempo proporcional a la altura del árbol, y los árboles binarios de búsqueda ordinarios pueden tomar alturas muy grandes en situaciones normales, como cuando las claves son insertadas en orden. Mantener baja la altura se consigue habitualmente realizando transformaciones en el árbol, como la rotación de árboles, en momentos clave.
Tiempos para varias operaciones en términos del número de nodos en el árbol n:
| Operación | Tiempo en cota superior asintótica |
| Búsqueda | O(log n) |
| Inserción | O(log n) |
| Eliminación | O(log n) |
| Iteración en orden | O(n) |
Para algunas implementaciones estos tiempos son el peor caso, mientras que para otras están amortizados.
Estructuras de datos populares que implementan este tipo de árbol:
Árbol binario
Árbol binario
En ciencias de la computación, un árbol binario es una estructura de datos en la cual cada nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda, los montículos binarios y Codificación de Huffman.
En ciencias de la computación, un árbol binario es una estructura de datos en la cual cada nodo siempre tiene un hijo izquierdo y un hijo derecho. No pueden tener más de dos hijos (de ahí el nombre "binario"). Si algún hijo tiene como referencia a null, es decir que no almacena ningún dato, entonces este es llamado un nodo externo. En el caso contrario el hijo es llamado un nodo interno. Usos comunes de los árboles binarios son los árboles binarios de búsqueda, los montículos binarios y Codificación de Huffman.
Árbol (informática)
Árbol (informática)
En ciencias de la informática, un árbol es una estructura de datos amplia mente usada que imita la forma de un árbol (un conjunto de nodos conectados). Un nodo es la unidad sobre la que se construye el árbol y puede tener cero o más nodos hijos conectados a él. Se dice que un nodo  es padre de un nodo
es padre de un nodo  si existe un enlace desde
si existe un enlace desde  hasta
hasta  (en ese caso, también decimos que
(en ese caso, también decimos que  es hijo de
es hijo de  ). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos se conoce como hoja. Los demás nodos (tienen padre y uno o varios hijos) se les conoce como rama.
). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos se conoce como hoja. Los demás nodos (tienen padre y uno o varios hijos) se les conoce como rama.
 es padre de un nodo
es padre de un nodo  si existe un enlace desde
si existe un enlace desde  hasta
hasta  (en ese caso, también decimos que
(en ese caso, también decimos que  es hijo de
es hijo de  ). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos se conoce como hoja. Los demás nodos (tienen padre y uno o varios hijos) se les conoce como rama.
). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos se conoce como hoja. Los demás nodos (tienen padre y uno o varios hijos) se les conoce como rama.domingo, 27 de octubre de 2013
Recursividad
Recursividad
Un algoritmo recursivo es un algoritmo que expresa la solución de un problema en términos de una llamada a sí mismo. La llamada a sí mismo se conoce como llamada recursiva o recurrente.
Generalmente, si la primera llamada al subprograma se plantea sobre un problema de tamaño u orden N, cada nueva ejecución recurrente del mismo se planteará sobre problemas, de igual naturaleza que el original, pero de un tamaño menor que N. De esta forma, al ir reduciendo progresivamente la complejidad del problema que resolver, llegará un momento en que su resolución sea más o menos trivial (o, al menos, suficientemente manejable como para resolverlo de forma no recursiva). En esa situación diremos que estamos ante un caso base de la recursividad.
Las claves para construir un subprograma recurrente son:
- Cada llamada recurrente se debería definir sobre un problema de menor complejidad (algo más fácil de resolver).
- Ha de existir al menos un caso base para evitar que la recurrencia sea infinita.
Es frecuente que los algoritmos recurrentes sean más ineficientes en tiempo que los iterativos aunque suelen ser mucho más breves en espacio.
- Definición : Propiedad de las funciones (Métodos) de auto llamarse, son una alternativa a los procesos iterativos.
- Utilidad : Cuando los procesos iterativos son muy complejos.
- Aplicación : Recorrido de estructuras no lineales, solución de ecuaciones matemáticas complejas.
- Implementacion :
FUNCIÓN Factorial(n)
VAR resultado: Entero
SI (n<2) ENTONCES
resultado = 1;
SINO
resultado = n * Factorial(n-1);
FSI
RETORNA resultado;
FFUNCIÓN
Cola Circular BICOLA
Bicola
La bicola o doble cola es un tipo de cola especial que permiten la inserción y eliminación de elementos de ambos extremos de la cola.
Puede representarse a partir de un vector y dos índices, siendo su representación más frecuente una lista circular doblemente enlazada.
Suscribirse a:
Comentarios (Atom)